OPTIONAL HALO ORBITS
IN SNELSON'S ATOM
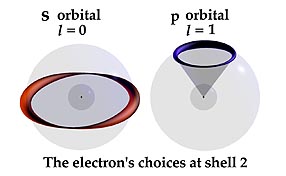
The de Broglie standing
wave is extended in Snelson's model to provide the required orbital choices
for the electron. These are shown as libration point, halo orbits. They
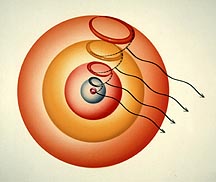
come about by this principle: At the left is the de Broglie orbit of the
hydrogen atom's shell number two. Two standing waves surround the nucleus.
Each wave is unique to this energy surface; twice as long as the wave
in the first shell. Because this orbit is at the shells' equator it has
no preferred direction in respect to the nucleus. It can move over the
electrical shell to occupy the entire sphere. |
| At
the right is the optional one-wave halo orbit of Snelson's model. Its
single wave is identical to one of the waves of the two-wave state. Because
it cannot surround the shell's girth it travels only a small circle portion
of it. It has achieved a direction in space, "reaching out"
from the nucleus even though it remains on the same sphere as the equatorial
orbit. Because its path is half as long, it completes its orbit at twice
the speed of the two-wave state. This provides it with double the top-like
angular momentum, and orbital magnetic force of the larger orbit. |
 |
HOW MIGHT AN ELECTRON REMAIN
IN A SMALL CIRCLE HALO ORBIT?
|
|
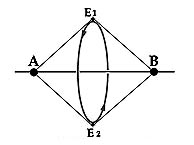
Niels Bohr originally
introduced the idea of electrons in halo orbits, non-equatorial to the
nucleus. This was shown in his proposed model of the Hydrogen molecule
H2. He considered it as composed of two protons with a pair of shared
electrons in a common orbit lying midway between the two nuclei.
A similar structure
occurs in NASA's libration-point satellite, the International Sun-Earth
Explorer 3, which orbits in a place at a point of gravitational equilibrium
in between the Earth and the Sun.
|
 |
| In
Snelson's model, in a complex atom with many electrons, those in the same
shell provide one another with the supplemental force--their electrostatic
repelling charge--which is needed to create a libration point electron
orbit. Moreover, since the electrons are unable to interpenetrate one
another's matter-wave, this barrier is the associated phenomenon by which
the orbits limit one another on the shells' surface. |
|
In the hydrogen
atom there is no such supplemental force available to sustain the electron
in a halo orbit. These states are therefore but momentary, transitory
conditions. They can be likened to a "shelf" onto which the
electron is deflected by incoming light from a direction. After landing
at one of these levels where it is able to form a wave, it will fall
at once back to a lower level.
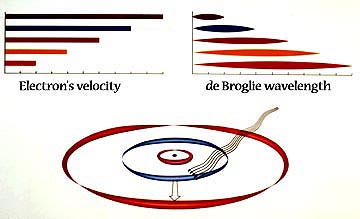
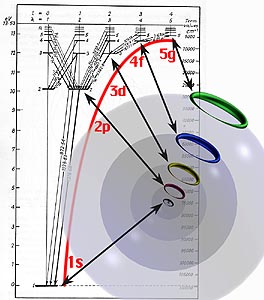
Shown here are
the one-wave states for five consecutive shells, as the electron drops
from one to the next with the emission of light of a certain color.
The energy states in the electron's fall would be from the 5g to 4f
to 3d to 2p to the 1s ground state.
|
 |
|
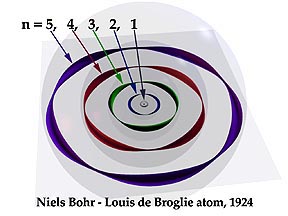
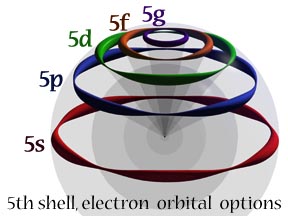
This picture represents
the hydrogen atom's fifth shell with the five possible excited states
the electron can choose from, according to Snelson's model. The orbit
at the equator is de Broglie's original orbit with its five standing
waves. By maintaining the same length of the individual waves, the other
four, libration-point orbits are created by the systematic removal of
whole waves; one for each smaller orbit. This makes available a four-wave
orbit (5p), a three-wave orbit (5d), a two-wave orbit (5f), and the
final one-wave state (5g).
While the electron's
linear velocity does not change with each shorter pathway, the number
of cycles per second is increased in jumps, to the maximum in the one-wave
orbit. This has the effect of increasing the orbital angular momentum
as well as the orbital magnetism.
|
 |
|
Sections: 1
2
3
4
5
6
7
8
|