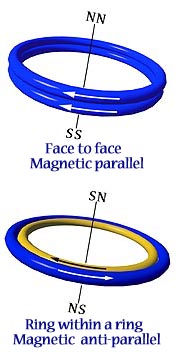
SNELSON REPRESENTS ELECTRON PAIRING IN TWO WAYS In addition to lying edge to edge in antiparallel, there are two alternate ways for ring-shaped magnets to form attractive relationships. 1. If two magnets are placed one on top of another, in parallel, they will attract face to face. (Fig. on left) The fields add together as a double strength magnet. 2. If two magnets are of different diameters, so that one can fit within the other as a ring within a ring, they will attract if antiparallel. (Fig. on right) If the magnets are of the same strength, they cancel one another to zero. 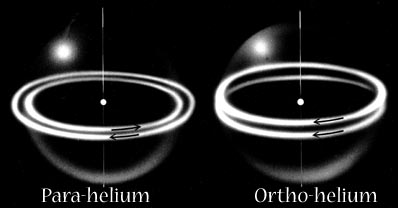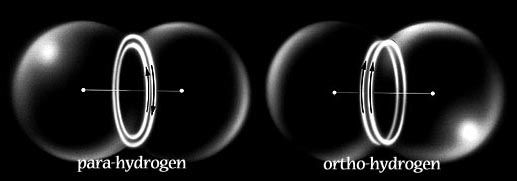In Snelson's model these become the two modes of magnetic attraction by which electrons can pair together, either in the covalent bond or in the outer shell configurations of the noble gases.

PAIRS OF ELECTRONS; HELIUM AND HYDROGEN Snelson represents the two different electronic states of Helium as different magnetic relationships for the electron orbits. In a similar manner, Snelson represents two structures for the Hydrogen Molecule. This bears resemblance to Bohr's original model with two protons sharing a pair of electrons, in orbit between them. In Snelson's picture, the two electrons occupy exclusive orbits which associate magnetically either in parallel (ortho-Hydrogen), or in antiparallel (para-Hydrogen).

THE INERT GAS SHELL The noble gas configuration is represented by Snelson as a tetrahedral structure composed of four pairs of magnetically antiparallel orbits. Most molecules are not geometrically regular. In H2O for example, the two hydrogen atoms sit at 104 1/2 degrees to one another instead of the proper tetrahedral angles of 109 1/2 degrees. In Snelson's model these "bent" angles result from the geometric properties of differently sized circles.
By taking two pennies and two dimes, one can hold them to form a spherical closure -- a tetrahedron. But, because the dimes are smaller than the pennies they form a more acute angle in respect to the sphere's center. Snelson describes the H2O molecule as like the Neon structure except that the two hydrogen protons are at the centers of two of the tetrahedral faces. These positive fields draw in their pairs of electrons, making these circles smaller, deforming the symmetry into what could be described as "bent" bonds.
Sections: 1 2 3 4 5 6 7 8