|
Snelson has discovered
a unique set of seven symmetry arrangements which permit identical circular
magnets to link continuously on a sphere. They contain 2, 5, 8, 10, 14,
18 or 32 magnets. He uses these to represent magnetic arrangements where
electrons link up to form systems of lower energy.
Snelson's explanation
for his magnetic structures: "In regard to the magnetic aspects of
my model, it is often pointed out that the orbital magnetic field of the
electron is puny -- about 1/100th the strength of the electrostatic force,
which would tend to push electrons away from one another. How, then, can
such small magnetic fields urge them into proximity? What this over-looks
is the atomic condition of electrons.
Yes, they repel one
another, and would perhaps prefer not to be so close together within the
atom. But it is their lot to be confined by the nuclear electrical field
which, electrically, they 'balance out'. They make the otherwise positive
nuclear sphere an electrical `gray'; that is, neutral. Now, this in no
way diminishes nor abates the magnetic forces.
These are no longer
in a contest of strength with the repelling electrostatic forces. The
nucleus has already forced the electrons to exist together. In this state,
therefore, they must make the best of the situation and arrange their
magnetic fields as economically as possible to conserve energy."
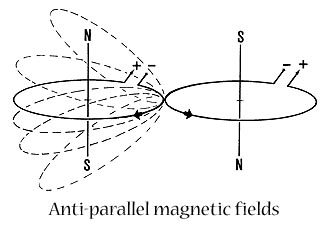
The small arrows
near the circles on the previous page indicate the directions the electrons
would move in order to give rise to adjacent antiparallel magnetic fields
they operate in counter-rotating directions like gears
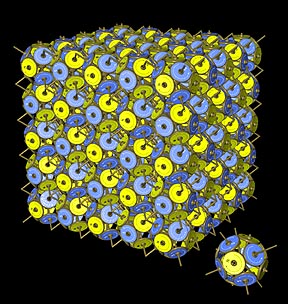
Because these spherical
forms have symmetry properties like polyhedra, with the planes of cubes
and other geometrical shapes, they can form larger forms by joining at
common magnetic faces. three such patterns are shown here.


|